Suponiendo diodos ideales, determinar y representar la función de transferencia Io = f(Vi), indicando en cada zona el estado de los diodos, con R=750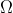
, VR1=VR2, RL = 250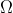
Solución: Primero debemos entender, que dependiendo el valor de Vi puede modificarse el comportamiento del circuito. Vi puede ser negativo o positivo, pero solo existirá un valor donde el diodo 1 se encienda o apague; e igualmente con el diodo 2.
Supongamos que Vi es una fuente alterna de señal senuidal. Tendriamos que ver como reacciona el circuito cuando Vi>>0, Vi=0 y Vi<<0. (Los estudiaremos por etapas).
Primera etapa: Vi<<0 (D1 ON y D2 OFF)
Va es menor a Vf y por ende Vb < Ve , Vc<Vd ,debido que Vb es el cátodo de D1 y Ve es el ánodo de D1, diodo 1 estará encendido (cuando A>K el diodo esta en ON). Inversamente con diodo 2, (K>A D2 OFF).
El circuito nos queda:
Nos damos cuenta que la fuente VR1 fija la tensión entre los puntos e y b (Ve>Vo) que será la tensión en los extremos de la resistencia. Aplicando ley de Ohm RL, entonces Io:
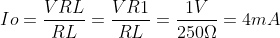
Ya habiamos establecido el sentido de
Io negativo para
Vi<0, entonces
Io= -4mA
Segunda etapa: D1 y D2 estan apagados
Después que el voltaje de la fuente llega a su valor pico negativo, comienza hacerse menos negativo hasta alcanzar su máximo posito. Debemos determinar el valor de Vi para cuando D1 se apague aún siendo menor que cero.
Entonces el circuito nos queda:
Nos queda 2 resistencias en serie, asi que Vi será:
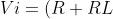(Io)&space;=&space;-4&space;V "Vi=(R+RL)(Io) = -4 V")
D1 se apagará para voltajes mayores o igual a -4 voltios.
Tercera etapa: Vi>>0 (D1 OFF y D2 ON)Aplicando el mismo procedimiento nos queda:
Io = 4mA y D2 se apaga a partir que
..
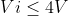
La función de transferencia será:
Extra: Si, ahora nos piden el valor medio de ID2.
Tenemos que ID2 en el tiempo es:
 |
| Se establecio que la señal inicia en cero por razones de cálculo. |
ID2 posee tres etapas, por ende para hallar el valor medio necesitamos realizar tres integrales y sumar los resultados de las mismas.
+&space;ID2&space;+&space;Imax\sin&space;\left&space;(&space;wt&space;\right&space;)&space;\right&space;\}dt "Im=\frac{1}{\tau }\int_{0}^{\frac{\tau }{2} }\left \{ Imax\sin \left ( wt \right )+ ID2 + Imax\sin \left ( wt \right ) \right \}dt")
Para determinar Imáx
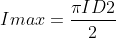
Imáx se 6,3 mA
Necesitamos obtener los valores de t1 y t2 de la grafica de ID2 en el tiempo. Para este fin, igualaremos (Imáx)(Senwt) con ID2, y despejaremos a t.
\left&space;(&space;\sin&space;\left&space;(&space;wt&space;\right&space;)&space;\right&space;)=ID2 "\left ( Imax \right )\left ( \sin \left ( wt \right ) \right )=ID2")
Sustituyendo nos queda:
Despejamos a t
 "wt=\sin^{-1}\left ( \frac{4mA}{6,3ma} \right )")
Sabemos que:
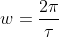
Ahora resulta sencillo hallar el valor medio de ID2.
Im= 3,12mA
Comentarios
Publicar un comentario