Dado el circuito:
a) Si conecta el interruptor S, en la posición 1; establezca la ecuación de corrientes de Kirchhoff
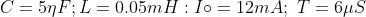
Resolución:
a) Si conecta el interruptor S, en la posición 1; establezca la ecuación de corrientes de Kirchhoff
Las corrientes que entran son igual a las corrientes que salen:
=&space;iR+&space;iC&space;+&space;iL "i\left ( t \right )= iR+ iC + iL")
Sustituyendo sus expresiones:
&space;=&space;\frac{V}{R}&space;+&space;C\frac{\mathrm{dV}&space;}{\mathrm{d}&space;t}&space;+&space;\frac{1}{L}\int&space;V\left&space;(&space;t&space;\right&space;)dt "i\left ( t \right ) = \frac{V}{R} + C\frac{\mathrm{dV} }{\mathrm{d} t} + \frac{1}{L}\int V\left ( t \right )dt")
b) Si la fuente esta desconectada ---- un corto tiempo
Derivamos la EDO y colocamos a i(t)=0
 "0= \frac{1}{R}\frac{\mathrm{dV} }{\mathrm{dt} } + C \frac{\mathrm{dV^{2}} }{\mathrm{dt^{2}} }+ \frac{1}{L}V\left ( t \right )")
Ordenando y dividiendo entre C
}{LC} "0= \frac{\mathrm{d^{2}} V}{\mathrm{dt^{2}} }+\frac{1}{RC}\frac{\mathrm{dV} }{\mathrm{dt} }+ \frac{V\left ( t \right )}{LC}")
Ahora podemos aplicar LAPLACE o resolver la EDO
por La transformada de LAPLACE nos queda:
=&space;S^{2}+\frac{1}{RC}S&space;+&space;\frac{V}{LC} "S\left ( 12 \right )= S^{2}+\frac{1}{RC}S + \frac{V}{LC}")
=&space;\frac{\frac{-1}{RC}\pm&space;\sqrt{\left&space;(&space;\frac{1}{RC}&space;\right&space;)^{2}-4\left&space;(&space;\frac{V}{LC}&space;\right&space;)}}{2} "S\left ( 12 \right )= \frac{\frac{-1}{RC}\pm \sqrt{\left ( \frac{1}{RC} \right )^{2}-4\left ( \frac{V}{LC} \right )}}{2}")
donde:
Si
Como no es muy intuitivo para algunos lectores mejor aplicaremos la otra opción
Podemos decir:
}{LC} "0=\frac{\mathrm{d^{2}V} }{\mathrm{d^{2}}t }+ \frac{2}{2RC}\frac{\mathrm{dV} }{\mathrm{dt} } + \frac{V\left ( t \right )}{LC}")
tenemos que:
Se espera que la solución homogénea es de la forma:
=&space;Ae^{pt} "V\left ( t \right )= Ae^{pt}")
Entonces nos queda:
=0 "Ae^{pt}\left ( p^{2} + 2\beta p+ \omega\circ ^{2}\right )=0")
aplicando la ecuación característica de la ecuación diferencia asociada, se tiene como raíces:
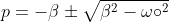
Ahora si queremos un amortiguamiento critico:
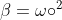
sobre-amortiguado:
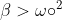
sub-amortiguado:
 |
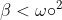
| Circuito RCL en paralelo |
b)Al colocar el interruptor S en la posición 1 --- en un tiempo muy largo --- el condensador C se carga a un valor Q(infinito). Si luego cambiamos al interruptor S en la posición 2, --- desconectamos la fuente ---: encuentre :
1) El valor de Rc para que el amortiguamiento sea critico. 2) Si Rc disminuye en 10% el valor anterior, Que tipo de amortiguamiento se tiene? 3) Cuanto vale la perdida de energía por ciclo? 4) Con los valores, Q(0)=0 y Q`(0)= I(0)= 1 mA, encuentre la solución homogénea, de la ecuación obtenida en 1a.
2) Si ahora se conecta el generador con una fuente sinusoidal de valor I(t) = Io. Sen(w`t ) encuentre:
a) Frecuencia de resonancia
b) La amplitud del voltaje y la fase en función de la frecuencia
c) Energía almacenada por la inductancia y el condensador
d) La perdida de energía disipada
Aplicación numérica
Resolución:
a) Si conecta el interruptor S, en la posición 1; establezca la ecuación de corrientes de Kirchhoff
Las corrientes que entran son igual a las corrientes que salen:
Sustituyendo sus expresiones:
b) Si la fuente esta desconectada ---- un corto tiempo
Derivamos la EDO y colocamos a i(t)=0
Ordenando y dividiendo entre C
Ahora podemos aplicar LAPLACE o resolver la EDO
por La transformada de LAPLACE nos queda:
donde:
| pulsación propia |
| decremento logarítmico |
Si
| Amortiguamiento critico |
| Sobre amortiguado |
| Sub- Amortiguado |
Como no es muy intuitivo para algunos lectores mejor aplicaremos la otra opción
Podemos decir:
tenemos que:
| pulsación propia |
| decremento logarítmico |
Entonces nos queda:
aplicando la ecuación característica de la ecuación diferencia asociada, se tiene como raíces:
Ahora si queremos un amortiguamiento critico:
sobre-amortiguado:
sub-amortiguado:
Publicado por:
 |
| 🎓בן האלוהים |
Comentarios
Publicar un comentario